"all finite relatively static knowledge can be represented in the BKO scheme"
If I was a real computer scientist or mathematician I would prove that claim. But I'm a long way from that, so the best I can offer is, "it seems to be the case with the examples I have tried so far". Yeah, vastly unsatisfying compared to a real proof.
And a couple of notes:
1) BKO is what I call an "active representation". Once in this format a lot of things are relatively easy. eg, working with the IMDB data was pretty much trivial.
2) One of the driving forces behind BKO is to try and collapse all knowledge into one general/unified representation (OP KET => SUPERPOSITION). The benefit being that if you develop machinery for one branch of knowledge it often extends easily to other branches.
3) The next driving force is efficiency of the notation. So while my results are possible to reproduce using other methods, BKO notation is more efficient. One benefit of the correct notation is if you make a hard thing easier, you in turn make a harder thing possible. eg, in physics there are notational short-cuts all over the place for just this reason.
4) Another selling point for the BKO notation is how closely English maps to it.
How about a summary of some examples that show how clean and powerful the notation is:
Learning plurals:
plural |word: *> #=> merge-labels(|_self> + |s>) plural |word: foot> => |word: feet> plural |word: mouse> => |word: mice> plural |word: radius> => |word: radii> plural |word: tooth> => |word: teeth> plural |word: person> => |word: people>Some general rules that apply to all people:
siblings |person: *> #=> brothers |_self> + sisters |_self> children |person: *> #=> sons |_self> + daughters |_self> parents |person: *> #=> mother |_self> + father |_self> uncles |person: *> #=> brothers parents |_self> aunts |person: *> #=> sisters parents |_self> aunts-and-uncles |person: *> #=> siblings parents |_self> cousins |person: *> #=> children siblings parents |_self> grand-fathers |person: *> #=> father parents |_self> grand-mothers |person: *> #=> mother parents |_self> grand-parents |person: *> #=> parents parents |_self> grand-children |person: *> #=> children children |_self> great-grand-parents |person: *> #=> parents parents parents |_self> great-grand-children |person: *> #=> children children children |_self> immediate-family |person: *> #=> siblings |_self> + parents |_self> + children |_self> friends-and-family |person: *> #=> friends |_self> + family |_self>Asking about Fred:
"Who are Fred's friends?" friends |Fred> "What age are Fred's friends?" age friends |Fred> "How many friends does Fred have?" how-many friends |Fred> "Do you know the age of Fred's friends?" do-you-know age friends |Fred> "Who are Fred's friends of friends?" friends friends |Fred> "What age are Fred's friends of friends?" age friends friends |Fred> "How many friends of friends does Fred have?" how-many friends friends |Fred> ... and so on.Some movie trivia:
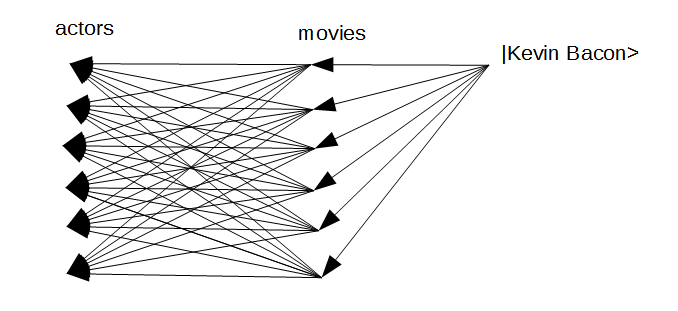
"What movies do Matt Damon and Morgan Freeman have in common?" common[movies] (|actor: Matt Damon> + |actor: Morgan (I) Freeman>) movie: Invictus (2009) movie: The People Speak (2009) movie: Magnificent Desolation: Walking on the Moon 3D (2005) "What actors do "Ocean's Twelve" and "Ocean's Thirteen" have in common?" common[actors] (|movie: Ocean's Twelve (2004)> + |movie: Ocean's Thirteen (2007)> ) actor: Don Cheadle actor: Casey Affleck actor: Elliott Gould actor: Bernie Mac actor: Matt Damon actor: Brad Pitt actor: Eddie Izzard actor: Eddie Jemison actor: George Clooney actor: Scott Caan actor: Jerry (I) Weintraub actor: Scott L. Schwartz actor: Carl Reiner actor: Shaobo Qin actor: Andy (I) Garcia actor: Vincent CasselKevin Bacon numbers:
kevin-bacon-0 |result> => |actor: Kevin (I) Bacon> kevin-bacon-1 |result> => actors movies |actor: Kevin (I) Bacon> kevin-bacon-2 |result> => [actors movies]^2 |actor: Kevin (I) Bacon> kevin-bacon-3 |result> => [actors movies]^3 |actor: Kevin (I) Bacon> kevin-bacon-4 |result> => [actors movies]^4 |actor: Kevin (I) Bacon>Working with a grid:
sa: load 45-by-45-grid.sw sa: near |grid: *> #=> |_self> + N|_self> + NE|_self> + E|_self> + SE|_self> + S|_self> + SW|_self> + W|_self> + NW|_self> sa: building |grid: 4 40> => |building: cafe> sa: create inverse sa: current |location> => inverse-building |building: cafe> -- now ask what is your current location? sa: current |location> |grid: 4 40> -- what is near your current location? sa: near current |location> |grid: 4 40> + |grid: 3 40> + |grid: 3 41> + |grid: 4 41> + |grid: 5 41> + |grid: 5 40> + |grid: 5 39> + |grid: 4 39> + |grid: 3 39> -- what is 3 steps NW of your current location? sa: NW^3 current |location> |grid: 1 37> -- what is near 3 steps NW of your current location? -- NB: since we are at the edge of a finite universe grid, there are less neighbours than in other examples of near. -- this BTW, makes use of |> as the identity element for superpositions sa: near NW^3 current |location> |grid: 1 37> + |grid: 1 38> + |grid: 2 38> + |grid: 2 37> + |grid: 2 36> + |grid: 1 36> -- what is 7 steps S of your current location? sa: S^7 current |location> |grid: 11 40> -- what is near 7 steps S of your current location? sa: near S^7 current |location> |grid: 11 40> + |grid: 10 40> + |grid: 10 41> + |grid: 11 41> + |grid: 12 41> + |grid: 12 40> + |grid: 12 39> + |grid: 11 39> + |grid: 10 39>Working with ages:
age-1 |age: *> #=> arithmetic(|_self>,|->,|age: 1>) age+1 |age: *> #=> arithmetic(|_self>,|+>,|age: 1>) almost |age: *> #=> age-1 |_self> roughly |age: *> #=> 0.5 age-1 |_self> + |_self> + 0.5 age+1 |_self> -- almost 19: sa: almost |age: 19> |age: 18> -- roughly 27: sa: roughly |age: 27> 0.500|age: 26> + |age: 27> + 0.500|age: 28>Learning indirectly:
-- set our "you" variable: sa: |you> => |Sam> -- learn your age: sa: age "" |you> => |age: 23> -- ask Sam's age: sa: age |Sam> |age: 23> -- greet you: sa: random-greet "" |you> |Good morning Sam.>And that pretty much concludes phase 1 of my write-up. Heaps more to come!
Update: here is a fun example of the right notation making things easier.
Consider algebra, but using Roman not Arabic numerals:
27x^3 + 78y + 14
vs:
XXVII * x^3 + LXXVIII * y + XIV
or alternatively consider trying to read a large matrix with values written in Roman numerals. Ouch!
Update: we can do all the above examples using just these key pieces:
OP KET => SUPERPOSITION
label descent, eg: |word: *>, |person: *>, |grid: *>, |age: *>
stored rules, ie: #=>
merge-labels()
|_self>
common[OP] (|x> + |y>)
load file.sw
create inverse
|> as the identity element for superpositions
arithmetic()
learning indirectly, eg: age "" |you> => |age: 27>
pick-elt (inside random-greet)